Chapitre 3 - Dérivées et sens de variations
Les courbes qui peuvent représenter de nombreuses situations d'études intéressantes (évolution d'une population, variations de salaire, taux d'emploi) donnent de nombreux indices graphique :
- Une zone croissante peut indiquer une hausse de prix
- Une zone décroissante peut indiquer le recul d'une épidémie
- Un maximum peut indiquer le moment plus ensoleillé de l'année
- Un minimum peut indiquer le moment le moins bénéfique de l'année pour une entreprise
Ces différentes observations graphiques peuvent être validées par outil de calcul sur les fonctions : les dérivées.
IIntroduction : nombre dérivé et tangente
Le nombre dérivé a une interprétation géométrique :
Le nombre dérivée \(f '(a)\) est le coefficient directeur de la droite tangente (si elle existe) à la
courbe en \(x=a\).
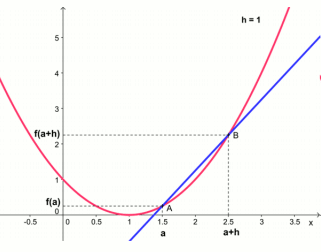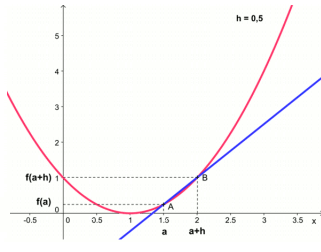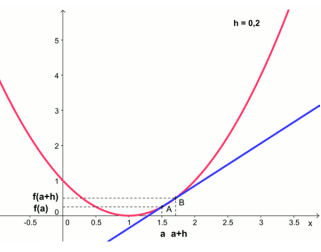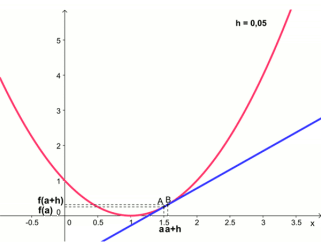
- Si \(f'(a) \gt 0\), alors la courbe est croissante autour du point d'abscisse \(x=a\)
- Si \(f'(a) \lt 0\), alors la courbe est décroissante autour du point d'abscisse \(x=a\)
IIDérivée de fonctions
1Définition de fonction dérivée
Soit \(f\) une fonction définie sur un intervalle \(I\).
Si \(f\) admet un nombre dérivé \(f'(x)\) pour tout \(x\) de\(I\), alors on dit que \(f\) est dérivable
On note \(f'\) sa fonction dérivée, la fonction qui pour tout \(x\) détermine le nombre dérivé \(f'\)
2Dérivées des fonctions usuelles
On note \(f'\) la dérivée de la fonction \(f\) :
$$ \begin{array}{|c|c|c|c|} \hline f & f' & f \text{ définie sur} \\\hline k \text{ (constante)} & 0 & \mathbb{R} \\\hline x & 1 & \mathbb{R} \\\hline x^2 & x & \mathbb{R} \\\hline x^3 & 3x^{2} & \mathbb{R} \\ \hline x^n & nx^{n-1} & \mathbb{R} \text{ où }(n\geq 0) \\ \hline\hline \frac{1}{x} &\frac{-1}{x^2} & ]0;+\infty[ \text{ ou } ]\infty;0[ \\\hline \frac{1}{x^n} & \frac{-n}{x^{n+1}} & ]0;+\infty[ \text{ ou } ]\infty;0[ \text{ où }(n\geq 0) \\ \hline\hline \sqrt{x} & \frac{1}{2\sqrt{x}} & \begin{array}{cc} f \text{définie sur }[0;+\infty[\\ \text{et dérivable sur }]0;+\infty[\end{array} \\\hline \end{array}
$$
3Opérations sur les fonctions dérivables
Soient \(f\) et \(g\) deux fonctions dérivables et \(k\) un nombre réel :
- \((f+g)'=f' + g'\)
- \((f-g)'=f' - g'\)
- \((k f)'=k f'\)
Si \(u (x) = x^2\) et \(v (x) = x\) :
- Si \(f (x) = u (x) + v (x)\), alors la dérivée \(f '(x) = 2 x + 1\)
- Si \(g (x) = u (x) - v (x)\), alors la dérivée \(g '(x) = 2 x - 1\)
- Si \(h (x) = 3 u (x)\), alors la dérivée \(h '(x) = 3 \times 2 x = 6 x\)
IIISens de variations et dérivées
1Sens de variations
La signe de la fonction dérivée nous permet de déduire les variations de la fonction de départ :
\(f\) est dérivable, définie sur un intervalle \(I\) :
- Si \(f'\) est positive sur \(I\), alors \(f\) est croissante sur \(I\)
- Si \(f'\) est négative sur \(I\), alors \(f\) est décroissante sur \(I\)
- Si \(f'\) est nulle sur \(I\), alors \(f\) est constante sur \(I\)
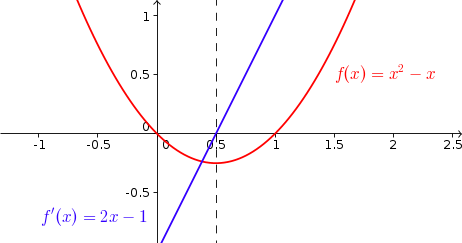
On trace la fonction d'équation \(f (x) = x^2 - x\) et sa dérivée \(f'(x) = 2 x - 1\) :
 On observe en effet que :
On observe en effet que :
 On observe en effet que :
On observe en effet que :
- Pour \(x \lt 0,5\), \(f'(x) \lt 0\) et \(f\) est décroissante
- Pour \(x \gt 0,5\), \(f'(x) \gt 0\) et \(f\) est croissante
2Extremum local
Un extremum local (ou global) est soit un minimum local (ou global), soit un maximum local (ou global).
On représente une fonction \(f\) ci-dessous avec \(5\) extrema :
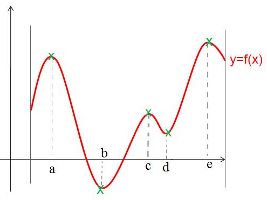
- La fonction \(f\) présente des maxima locaux en \(a\), \(c\) et \(e\)
- La fonction \(f\) présente des minima locaux en \(b\) et \(d\)
- La fonction \(f\) présente un maximum global en \(e\) et un minimum global en \(b\)
Tableau de variations de la fonction :
$$ \begin{array}{c|lcccr|} x & & & a & & b & & c & & d & & e & \\\hline f (x) & & \nearrow & & \searrow & & \nearrow & & \searrow & & \nearrow & & \\ \end{array}
$$